General description
Program system TMODES is formed in order to present the movement simulation results of the robotic mechanism with elastic segment in the presence of higher harmonicas (second mode) on the principles set out in the papers [1]-[6]. That confirmed the necessity to expand Euler-Bernoulli equation from many aspects after two and a half centuries. In fact for many years the Euler-Bernoulli equation has been used in its original form, which cannot be justified concerning the knowledge from robotics, theory of oscillation, theory of elasticity that has been gathered by generations as well unavoidable computer support. A new form of the Euler-Bernoulli equation has been formed through this program package so that “assumed modes technique” was not used but new principles based on the classic mechanics laws have been formed. Results generated by the program system TMODES are the proof of the theoretical foundations that a new form of Euler-Bernoulli equation is based on as well as the classical form of mechanism mathematical model that follows directly by setting limiting conditions. The form of elastic deformation during the robot task realization, through presented simulations, is a result of the present forces and it is not formed in advance as in “assumed modes technique”. Program system TMODES is generated in a way that it can be expanded by the user’s demands and it also provides a possibility of implementation of different control laws. A hand-made mathematical model of the mechanism with 6 freedom degrees with elastic link in the presence of the second mode (author of this mathematical model is also Mirjana Filipovic) is used as a basis for forming this program package. The software package TMODES is formed in MATLAB and it can be used even for the further researches in the area of Robotics, Theory of elasticity and Theory of oscillations, as well as in the area of the control of robotic systems with rigid and elastic elements.
Designed program package is used for synthesis and analysis of robotic system with 6 freedom degrees presented in Figure 1. Robotic system is formed with simultaneous elastic motor gear and elastic link in the presence of higher harmonicas (two modes). There is a possibility of synthesis and analysis of the influence of dynamic external force on the movement dynamics of the observed robot. In the papers [1] and [2], the general form of the mathematical model of the robot with elastic segments (in the presence of higher harmonicas) has been published for the first time in the literature. A new form of the motor mathematical model is an integral part of this result which is also new in literature. In these papers “a new form of the Euler-Bernoulli equation” is defined and thus based on “the original form of the Euler-Bernoulli equation” but with significantly implemented robotics knowledge and all that on the basis of classical mechanics. For many years our contemporaries have been using the original form of the Euler-Bernoulli equation in inappropriate way, and thus, as a matter of fact, the information about the complexity of the observed mechanism motion has being lost. In the new form of the Euler-Bernoulli equation the value of elastic deformation and its frequency change depending on the present moments (inertial, Coriolis, centrifugal, gravitational, coupling moments between present modes, as well as the action of the dynamic external force) and they also depend on the mechanism configuration, mass, segment length of the reference trajectory selection, dynamic characteristics of motor movements, selection of control laws etc. Program system TMODES is used under different conditions in the papers [1]-[4]. It has been used to obtain and analyze simulation results which is a confirmation of established and published scientific theoretical theses regarding the new interpretation of the Euler-Bernoulli equation, its solution as well as a new form of motor mathematical model.
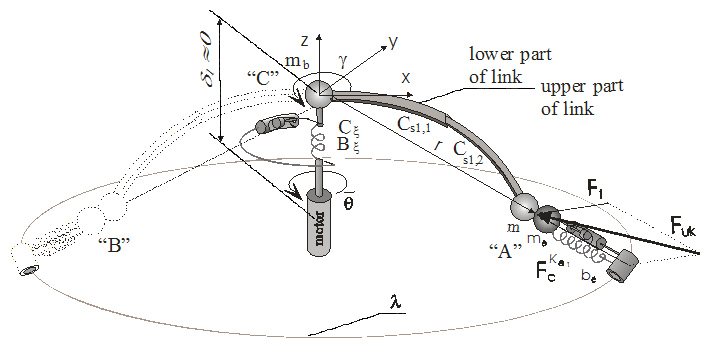
Fig. 1. Robot mechanism with elastic gear and elastic segment in the presence of higher harmonicas
Area to which technical solution refers
Robotics, Theory of elasticity and Theory of oscillations.
Problem being solved by the technical solution
This technical solution solves the problem of efficient implementation of the model robot with elastic segments in the presence of higher harmonicas including predesigned procedure for testing their behavior, as well as designed real conditions of robot task realization.
State of the problem solution in the world
In the literature the connection between the equation of motion in any elastic line points and Euler-Bernoulli equation has not been established but the point that these two approaches should have the completely different treatment has been set out.
The original form of the Euler-Bernoulli equation is defined under idealized conditions and it has a great theoretical importance. This equation does not have practical importance because the movements in mechanism do not take action under such idealized conditions. The original Euler-Bernoulli equation form, as well as its solution defined by Daniel Bernoulli, is defined for idealized conditions, i.e. presuming that oscillations are caused by disturbance force that is removed immediately. These equations are still used today in their original forms regardless the complexity of the observed robotic mechanism, which causes the loss of important information about the mechanism movement complexity.
In so far published literature, the general solution to the original form of Euler-Bernoulli equation, the elastic robotic system motion, and elastic deformations are also defined as transversal oscillations that can be found by the particular integral method of Daniel Bernoulli.
So far, the literature has not defined procedures for synthesizing the reference trajectory for the robotic system with elastic gears and elastic segments with simultaneous presence of the dynamic external force.
Until now, the rough approximation has been made with the assumption that the elastic effects are generated only by gravitational forces, or dynamics external force, or that the Coriolis’ and centrifugal forces are completely ignored so that the elastic discrepancies are so small that the inertial matrix does not depend on them.
40 years ago or precisely in 1967, Meirovitch appointed “assumed modes technique.
Author has elaborated a specific application of Euler-Bernoulli equation by which he assumed the elastic deformation as a value that is pre-defined by both amplitude and frequency, and so formed elastic deformation is entered in a dynamic model, which is absolutely illogical. It can be said that Meirovitch made the theses replacement.
The essence of technical solution
Nowadays, taking into consideration significantly improved knowledge in the robotics (classical mechanics); the Euler-Bernoulli equation can not be used anymore in its original form, as a purpose of synthesis and analysis of elastic robotic systems. Therefore, with respect to Euler and Bernoulli, it is necessary to further improve the equation. It is the only way for not losing information of complexity of movement dynamics of every mode within a segment (and broader within the total robotic configuration). Thus, it very important to connect the original Euler-Bernoulli equation and modern robotic knowledge on the principles of classical mechanics. The foundations of classical mechanics are particularly emphasized because synthesis and analysis of kinematics and dynamics of robotic configurations in stiff and elastic elements are based on them. The elasticity of segments on the principles of classical mechanics is implemented in this program system TMODES.
The meaning of this research has theoretical and practical
significance. The purpose is to define as realistically as possible
both kinematic and dynamic model of the mechanism with stiff and
elastic elements which will describe very well the real system.
In the papers [1] and [2] the general form of the mathematical model of
the robotic system with elastic segments, new form of the
Euler-Bernoulli equation is given for the first time. This research has
the aim to make known this topic to the scientific community through
modelling one example as well as to discover new phenomena in this
field.
The intensive development of the Robotics, especially strengthen by the development of data computer processing, has demanded and enabled that elastic deformation can be observed as a real dynamic value which depends on the system parameters.
Elastic deformation is a dynamic value by both amplitude and frequency and it is a result of the total system movement i.e. exterior and interior, dynamic and static forces.
The Robotics is very important because modeling of dynamics of robotic systems movements with rigid and elastic elements comes directly from it. We should emphasize the importance of further research, but now on the new principles set out in the papers [1] - [5] as well as in the program system TMODES.
Euler-Bernoulli equation was written in 1750. It was derived by
Bernoulli, physicist and Euler, mathematician, his lifelong friend and
associate. At that time they did not even dream about robotics and
knowledge that we now have now. However, although it was created more
than 250 years ago, Euler-Bernoulli equation is present even today and
it can be very logically connected with today’s robotics knowledge. I
especially emphasize robotics that, as mentioned before, is developing
very intensively, and in this case it imposes solutions to some other
areas such as the Theory of oscillations and the Theory of elasticity.
Here we have one of many innovations regarding the known assumptions.
In robotics the reference trajectory is defined in a clearly kinematics
i.e. geometrical way and now in the presence of elasticity elements in
defining reference trajectory we can also include values of elastic
deformations at the reference level i.e. at the level of knowing
elasticity characteristics. The same can be said for defining Jacobian
matrix and matrix of transformation.
This particularly important result opens up extensive possibilities for the application of different control laws, as well as the final opportunity to manage the position and orientation of the elastic robot peak in space.
Detailed description of characteristics
In this research new form of the Euler-Bernoulli equation has been defined and it has been directly derived from source form of the Euler-Bernoulli equation. During these researches, the knowledge from the robotic field has been included as well as from classical mechanics. Therefore, the result has been the new form of the Euler-Bernoulli equation as well as the new form of the mathematical model of the motor. Now, we have the difference in a structure of the Euler-Bernoulli equations new form for every mode as a consequence of the present forces which point to the intense coupling of modes. It confirms the full structure of a matrix of stiffness and damping not only in new form of the Euler-Bernoulli equation but in the equation of a mathematical model of the motor also. Damping is an omnipresent elasticity characteristic of real systems, so that it is naturally included in the Euler-Bernoulli equation new form. An elastic deformation is dynamic size and it naturally depends on disturbing forces as well as on stationary forces during the realization of a robot’s task.
Denavit-Hartenberg parameters of elastic robotic mechanism are defined, as well as transformation matrix, which represents the solution of the direct kinematics in Robotics. In that way, the possibility for defining a new form of the Jacobian matrix has been open as well as the formulation of the reference trajectory which includes the characteristics of elasticity at the level of the estimated values of stiffness and damping. Everything has been done according to the principles of classical mechanics.
References
[1] Mirjana Filipović and Miomir Vukobratović: "Complement of Source Equation of Elastic Line”, Journal of Intelligent & Robotic Systems, International Journal, Volume 52, No 2, (online April, June 2008) 233 - 261.
[2] Mirjana Filipović and Miomir Vukobratović: "Expansion of source equation of elastic line”, Robotica, International Journal, Volume 26, No 6, (online April, November 2008) 739-751.
[3] Mirjana Filipović "New form of the Euler-Bernoulli rod equation applied to robotic systems”, Theoretical and Applied Mechanics, Society Mechanics, Belgrade,2008, Volume35, No. 4, pp. 381-406.
[4] Mirjana Filipović, "Elastic deformation as a result of the total dynamics of the system Movements", 2nd International Congress of Serbian Society of Mechanics (IConSSM 2009)Palić (Subotica), Serbia, A-07, 1-5 June 2009, pp 1-14,.
[5] Mirjana Filipović, "Euler-Bernoulli Equation Today",
IROS 2009: IEEE/RSJ International Conference on Intelligent Robots and
Systems, St. Louis, MO, USA (11-15 October 2009), pp. 5691-5696.
[6] Mirjana Filipović, Ana Djuric, "Whole analogue between Daniel Bernoulli solution and direct kinematics solution”, Theoretical and Applied Mechanics, Society Mechanics, Belgrade, 2010, Volume 37, No.1, pp. 49-78.
