Research Topic: Extension of the Euler Bernoulli equation from many aspects
The Euler-Bernoulli equation and its solution were defined under the assumption that the elasticity force is opposed only by the inertial force proper. Besides, it is supposed by definition that the motion in Euler-Bernoulli equation is caused by an external force, suddenly added and then removed. The solution of D. Bernoulli satisfies these assumptions. The Euler-Bernoulli equation and its solution were defined under the assumption that the elasticity force is opposed only by the inertial force proper.
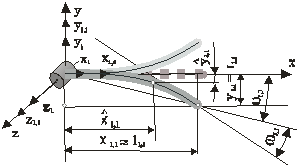
Fig. 1. Idealized motion of elastic body according to D. Bernoulli.
Besides, it is supposed by definition that the motion in Euler-Bernoulli equation is caused by an external force, suddenly added and then removed. The solution of D. Bernoulli satisfies these assumptions. Bernoulli presumed the horizontal position of the observed body as its stationary state (in this case it matches the position - axis). At such presumption, the oscillations happen just around the - axis. If Bernoulli, at any case, had included the gravity force in its equation, the situation would have been more real.

Fig. 2. Possible positions of the tip of elastic line with modes.
Then the stationery body position would not have matched the - axis position, but the body position would have been little lower and the oscillations would have happened around the new stationery position.The Euler-Bernoulli equation and its solution need a short explanation that, we think, should be assumed, but which is missing from the original literature. Euler and Bernoulli wrote your equation based on ‘vision’. They did not define the mathematical model of a link with an infinite number of modes, which has a general form, but they did define the motion solution (shape of elastic line) of such a link. They left the task of link modeling with an infinite number of modes to their successors.
Dynamics of each mode is described by one equation. The equations in the whole model are not of equal structure as our contemporaries, authors of numerous works, presently interpret it.We think that the coupling between the modes involved leads to structural diversity among the equations in the whole model. This explanation is of key importance and is necessary for understanding our further discussion.
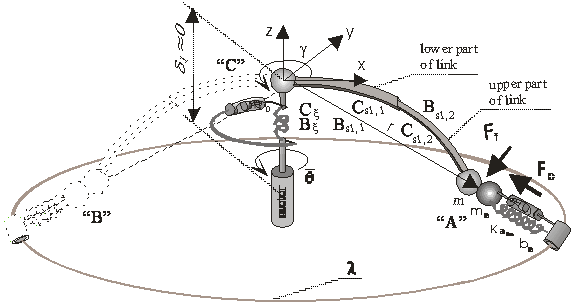
Fig. 3. Robot mechanism.
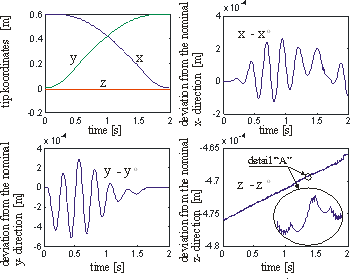
Fig. 4. The tip coordinates and the position deviation from the reference level.
The Bernoulli solution describes only partially the nature of motion of real elastic beams. More precisely, it is only one component of motion. The Euler-Bernoulli equation and its solution should be expanded from several aspects in order to be applicable in a broader analysis of elasticity of robot mechanisms. By supplementing these equations with the expressions that come out directly from the motion dynamics of elastic bodies, they become more complex.
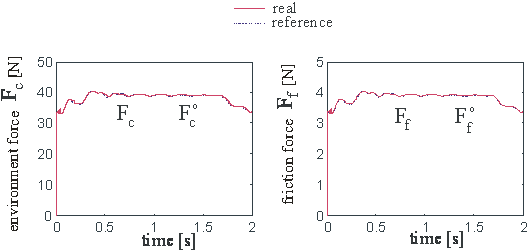
Fig. 5. The environment force dynamics.
The motion of the considered robotic system mode is far more complex than the motion of the body presented with Euler-Bernoulli equation. This means that the equations that describe the robotic system (its elements) must also be more complex than the equations formulated by Euler and Bernoulli. This fact is overlooked, and the original equations are widely used in the literature to describe the robotic system motion. This is very inadequate because valuable pieces of information about the complexity of the elastic robotic system motion are thus lost. Hence, it should be especially emphasized the necessity of expanding the source equations for the purpose of modeling robotic systems, and this should be done in the following way:
- based on the known laws of dynamics, Euler-Bernoulli equation is to be supplemented by all the forces that participate in the formation of the bending moment of the considered mode. It is assumed that the forces of coupling (inertial, Coriolis, and elastic) between the present modes are also involved, which yields structural difference between Euler-Bernoulli equation in the whole model.
- Structure of the stiffness matrix must also have the elements outside the diagonal, because of the existence of strong coupling between the elasticity forces involved.
- Damping is an omnipresent elasticity characteristic of real systems, so that it is naturally included in the Euler-Bernoulli equation.
- General form of the transversal elastic deformation is defined by superimposing particular solutions of oscillatory character (solution of Daniel Bernoulli) and stationary solution of the forced character (which is a consequence of the forces involved).
- General form of the elastic line, solution of the Euler-Bernoulli equation is a direct outcome of the dynamics of system motion and cannot be represented by one scalar equation but three equations are needed to define the position and three equations to define the orientation of each point on the elastic line.
- New structures of the stiffness matrix and mathematical model of actuators appear as a consequence of the coupling between the modes of particular links.
- Elastic deformation is a consequence of the overall dynamics of the robotic system, what is essentially different from the method that was used until today, which purports usage of “assumed modes technique”.
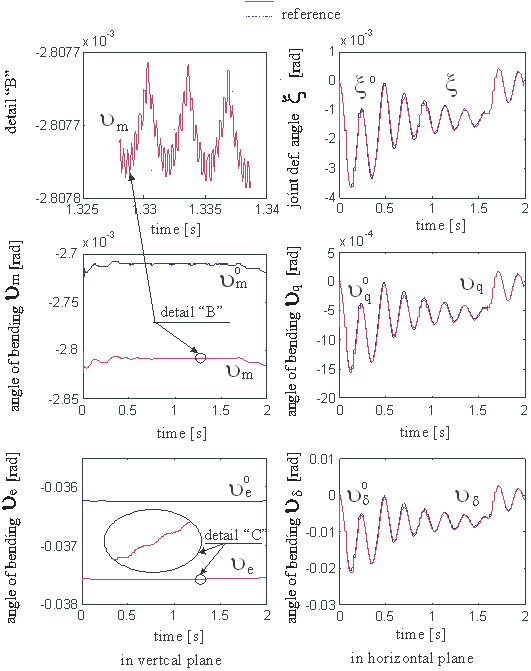
Fig. 6. The elastic deformations.
