General description
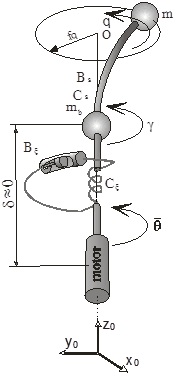
Fig. 1. Robotic mechanism.
This research area refers to the research which target is implementation and development, as well as extension of the implementation of the original form of Euler-Bernoulli equation of transverse oscillations of deformable beams for the purpose of synthesis and analysis of deformable elastic robotic systems or other types of elastic deformable mechanisms which have elastic beam segments in their construction. Motivation for the implementation of the elasticity characteristic, in the synthesis and analysis of the robotic elastic-deformable configuration consists of the following. Complex construction mechanisms are now commonly made of lightweight materials that are naturally characterized by flexibility, as well as elastic deformability. Fast and accurate movement of the mechanism is expected in the task realization. In many examples the constructions flexibility, as well as their deformability, appear as an obstacle for the precise and rapid movement control. The result of this research is to define the way of the implementation of elasticity and deformability properties in the construction, which should move quickly and precisely, with the use of highly authentic models. In this sense the possibility of using Euler-Bernoulli equation oscillations transversal of deformable prismatic beam oscillations was examined, but not in its original form, but in the new, extended, form for the implementation with the use of modern knowledge from robotics (based on the knowledge of classical mechanics). The propitiatory and confirmation of the method were also examined through the simulation results for a typical robotic elastic deformable configuration.
New approaches for the implementation of the Euler-Bernoulli equation, which are based on the knowledge of robotics and classical mechanics, are formulated. The starting point is the basic fact that the elastic deformation of dynamic values, which depends on the overall dynamics of robotic systems.
This means that the elongation, as well as the elastic deformation amplitude of the deformable rod and beams, robotic construction elements and the oscillation frequency change depending on the intensity of the dynamic force during the task implementation and that they also depend on the configuration of the elastic-deformable mechanism, mass distribution, length of segments, choice of reference trajectory, dynamic characteristics of the motor motion and so on. Connecting the original theory of Euler-Bernoulli on the basis of which the partial differential equation of transversal oscillations of elastic-deformable rods and prismatic beams are based, and contemporary knowledge from robotics the new significant results are achieved and the nonlinear dynamics phenomena of certain robot structures are discovered.
These new discoveries about on the nonlinear dynamics of deformable robotic structures are applied in the synthesis of the software package VERSPACE. The research goal was to define a more realistic dynamic model of the nonlinear-elastic deformable structures of the mechanism with the coupling of rigid and elastic elements that would reflect well enough the observed real system in Figure 1, and as a prerequisite for a good dynamic model it was necessary to define appropriate kinematic and kinetic model of the system. The formulation of the general form of the dynamic model of the observed mechanisms follows as the next result. The application of a new form of Euler-Bernoulli equation is demonstrated by generalization on the complex structure, as well as a new form of its solution, and new form of the motor mathematical model.
Simulation results generated by the software package VERSPACE give evidence to the theoretical assumptions, on which a new generalization of Euler-Bernoulli equation application is based, as well as the corresponding new form of solution of that application generalization on nonlinear dynamics of robotic elastic deformable structures, as well as a new form of the motor mathematical model. This important result opens widely the possibility to apply different control laws, as well as a final opportunity to manage the position and orientation of the top of the elastic robot in the space. This opens the field of geometric relationships management, unlike the present approaches to the management of the forces that act on the dynamic structure. Researches aim to approach this topic closer to the scientific and engineering public through modelling of the elasticity of the segments of the abstracted robot structure from the real system in the presence of higher harmonics, which is now in the pioneering research stage, discovering new phenomena of nonlinear dynamics in this field, first in the "simple" examples as it is analyzed, and then to be implement to the more complex robot configurations as well as to any other form of flexible mechanism, which does not have to look like a robotic one. The purpose of this research has both theoretical and practical significance.
Area to which technical solution refers
Robotics, Applied theory of oscillations and nonlinear dynamics in robotics, applied theory of elasticity in robotics.
Problem being solved by the technical solution
This technical solution solves the problem of the efficient synthesis and analysis of the models of robots with elastic link in the vertical plane as well as testing of its behavior under real simulation conditions of the robot task.
State of the problem solution in the world
45 years ago i.e. in 1967, Meirovitch prescribed “modal technique” (“assumed modes technique”). At that moment it was a huge contribution that was supposed to stimulate scientists to new speculations, new researches and new ideas. Then it was solution of one visionary who interpreted the Euler-Bernoulli equation in a new manner. That was supposed to be a flywheel in the evolution of the Theory of elasticity and the Theory of oscillation and, of course, Robotics which in that period was in expansion.
The author elaborated a particular application of the Euler-Bernoulli equation, supposing that elastic deformation was a value defined in advance according to the amplitude and frequency and, formed in this way, it was entered into the dynamic model.
Not finding any other solutions, many researchers in robotics, applied the Meiroitch’s solution in describing real dynamics of the robot system elastic deformations, overlooking the fact that the “assumed modes technique” solution was derived under the conditions:
- the elastic deformation defined in advance by both amplitude and frequency, and thus introduced into the model
- misinterpretations of Euler-Bernoulli equation solution.
The double substitution of thesis was done because the term "elastic deformation" was identified with the term "elastic line form", and these were two completely different values.
Until now the authors implemented the elastic deformation as a value based on the “assumed modes technique” principles and they did not get any real values as a result of the robot system movements. Not finding any other solutions it was obvious that the researches in this area were reduced in the last 15 years.
However, present development of, first of all, knowledge from the robot system dynamics modelling enables to establish and analyze new models which will treat the elastic deformation as a dynamic value. This research is directed in that way in order to describe this theory in the real environment, without assumptions i.e. limitations of the elastic deformation on which the “assumed modes technique” is based.
The essence of technical solution
The area which we deal with i.e. robotics is very important, because the modelling of the robot system movement dynamics with both rigid and elastic elements comes from it directly. The robotics is the area which can offer the solution and it represents the foundation of the further researches in many other areas. The reason for that is quite simple: the robotics progressed significantly in the last 40 years. It is important to emphasize the importance of the further researches which are now based on the new principles set in this program system VERSPACE and a series of publications until today.
The elastic deformation is a dynamic value which depends on the total dynamics of the robot system movements. That means that the elastic deformation amplitude and its frequency change depending on the forces (inertial forces, Coriolis, centrifugal forces, gravity forces as well as coupling forces between the present modes, and the play of the dynamic external forces). It, of course, depends also on the mechanism configuration, weight, length of the segments of the reference trajectory choice, dynamic characteristics of the motor movements etc.
The elastic deformation exists even in the state of inaction and then it depends on the gravity forces i.e. mechanism configuration. That means that the elastic deformation depends on the robot system characteristics and it can be calculated in any chosen moment. When we conduct the mechanism through the reference trajectory, the elastic deformation also exists but now at the reference level without the influence of the disturbance.
Euler-Bernoulli equation was written in 1750. It was written by Bernoulli, physicist and Euler, mathematician, his long-time friend and colleague. They did not even dream about the robotics and the knowledge we have now. But, although it was made more than 250 years ago, the Euler-Bernoulli equation is still actual and it can be connected logically with the contemporary knowledge from the robotics.
Detailed description of characteristics
The special attention is paid to the dynamics and kinematics motion of robotics configuration with elastic link in the vertical plane, which is really moving in space because of its elasticity. The kinematic model of the system presented in the Figure 1. (direct and inverse model) is created introducing the new definition of Denavit-Hartenbergs parameters. See Figure 2. The robot geometric between internal coordinates and the space of Cartesian coordinates (external coordinates) is defined as a “direct kinematics”.
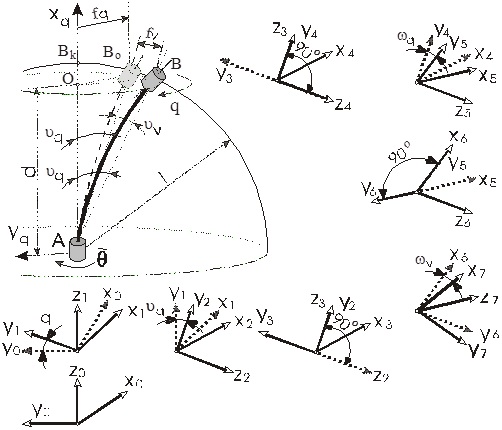
Fig. 2. Position of robot tip.
We demonstrated that the equation of balance of all the forces involved at any point (even at the point of the mode peak on the elastic line also) followed directly from the new form of Euler-Bernoulli equation. If we define boundary conditions for the mode peak as the most interesting point on the elastic line, we obtain the equation of balance at that point, i.e. a classical form of the mathematical model. The choice of the reference trajectory, which depends on the level of the knowledge of the elasticity characteristics, is generated. The estimated elasticity characteristics can be included in the reference trajectory as well as in the management law.
Euler-Bernoulli equation was expanded from several aspects.
With elastic robotic systems, the actuator torque is opposed by the bending moment of the first elastic mode, which is behind the motor, and partly by the bending moments of other modes, which are connected in series behind the observed motor. All modes, behind the motor, according to their position, influence the dynamics of motor motion. In the program system VERSPACE, the motor mathematical model is connected to the rest of the mechanism via the equivalent elasticity moment.
The analogue is applied between the solution of the Euler-Bernoulli equation defined by Daniel Bernoulli in its original form (i.e. solution of the extended form of Euler-Bernoulli equation) and the “direct kinematics solution” in Robotics. The connection between the original form of Euler-Bernoulli equation and its solution and modern knowledge in Robotics is established in the program system VERSPACE. See [1].
By this approach, the new research prospects have been opened.
Emphasis is placed on the importance of these results in the field of robotics, which develops very extensively and it becomes the inspiration in this research for the development of areas such as elastic-dynamics of robotic structures and dynamics of nonlinear phenomena and stability of robotic structures.
References
[1] Mirjana Filipovic, "The Procedure for the Application of a New Form of Euler-Bernoulli Equation and Its Solutions", 9th International Symposium on Intelligent Systems and Informatics - SISY 2011, Subotica, Serbia, ISBN 978-1-4577-1974-5, 8-10 September 2011. pp. 85-90. http://conf.uni-obuda.hu/sisy2011/
