General description

Fig. 1. Robotic mechanism.
This program system TIPEX, generated in MATLAB, developed on this level can be used for synthesis and analysis of the elastic robotic system in vertical plane from Fig 1. and it can be expanded from different aspects, according to the users’ needs. Nowadays, taking into consideration significantly improved knowledge in the robotics (classical mechanics); the Euler-Bernoulli equation can not be used anymore in its original form, as a purpose of synthesis and analysis of elastic robotic systems. Therefore, with respect to Euler and Bernoulli, it is necessary to further improve the equation. It is the only way for not losing information of complexity of movement dynamics of every mode within a segment (and broader within the total robotic configuration). Thus, it very important to connect the source form of Euler-Bernoulli equation and modern robotic knowledge on the principles of classical mechanics. The foundations of classical mechanics are particularly emphasized because synthesis and analysis of kinematics and dynamics of robotic configurations in stiff and elastic elements are based on them. The elasticity of segments on the principles of classical mechanics is implemented in this program system TIPEX.
The meaning of this research has theoretical and practical significance. The purpose is to define as realistically as possible both kinematic and dynamic model of the mechanism with stiff and elastic elements which will describe very well the real system.
In the papers [1]-[3] the general form of the mathematical model of the robotic system with elastic segments from Fig. 1, („New form of the Euler-Bernoulli equation”) is given for the first time. This program system TIPEX has the aim to make known this topic to the scientific community through modelling one example as well as to discover new phenomena in this field.
Area to which technical solution refers
Robotics, Theory of elasticity and Theory of oscillations.
Problem being solved by the technical solution
This technical solution solves the problem of efficient synthesis and analysis of robot model with elastic link in presence of second mode elements in its construction, as well as testing its behavior under simulated real conditions of robot task realization.
State of the problem solution in the world
Meirovitch proposed “modal technique” (“assumed modes technique”), more than 40 years ago, exactly in 1967. At that moment it was a big contribution supposed to stimulate scientists to new considerations, new investigations and new ideas. At that time it was solution by one visionary which explained Euler-Bernoulli equation in a new manner. It should have been a flywheel in the evolution of the Theory of elasticity and Theory of oscillation and also and Robotics which in this period was in expansion.
The author elaborated a particular application of the Euler-Bernoulli equation, supposing that elastic deformation is a quantity defined in advance with respect to amplitude and frequency and, formed in this way, included into dynamics model. Having in mind the state of engineering and the technical possibilities for data processing at that time, and also the technical needs at that time, this solution meant a very great contribution to science well as engineering. Regulations specifying the permissible amplitudes of elastic deformation and the permissible oscillating frequencies of constructions are employed even today in some areas of construction theory.
Those allowed values are mostly the result confirmed by various experience, measures and scientific solutions that were also based on Meiroitch’s theory. Thus it should be emphasized, that such solutions should not be denied in any case, but they should further be applied just in areas where it is not possible to form the system model, for example, because of its complexity.
Not finding any other solutions, many researchers in robotics, applied the Meiroitch’s solution in the description of the real dynamics of the robot system elastic deformations, overlooking that the “assumed modes technique” solution was derived under the condition of the elastic deformation defined in advance and by the amplitude and the frequency, or they used many ways to modify the same solutions.
By now the authors implemented the elastic deformations as the values on the “assumed modes technique” principles and they did not get any real values as a result of the robot system movements. Not finding any other solutions it is obvious that the researches in this area have been reduced in the last 10 years.
However, today’s development of the knowledge from the robot system dynamics modeling enables the establishing and analyzing of the new models which will treat the elastic deformation as the dynamic value. Our research filed is directed in that way, in order to describe this theory in the real environment, without assumptions i.e. limitations of the elastic deformation that is based on “assumed modes technique”.
With new knowledge collected through generations, the intensive development of the new technical areas such as robotics especially strengthen by the development of the data computing process, demanded and enabled that elastic deformation was considered really as the dynamic value which depended of the system parameters. The elastic deformation is a dynamic value by both amplitude and frequency and it is the result of the total system movement’s i.e. outer and inner, dynamic and static forces. Such elastic deformation should exist in the dynamics of the robot system movements. The synthesis of the robot system dynamics should be processed on the basis of the completely new different principles comparing to Meiroitch’s theory, with models based on the known, classic dynamics, the elasticity theory and the oscillation theory, where the elastic deformations are described as dynamic values of the inner and outer load which influence the total dynamics of the robot system movements.
The essence of technical solution
The area which we deal with, the robotics is very important, because the modeling of the robot system movement dynamics with both rigid and elastic elements comes from it directly. The robotics is the area which can offer the solution and it represents the foundation of the further researches in many other areas. The reason for that is quite simple: the robotics has progressed significantly in the last 40 years. It is important to emphasize the importance of the further researches but now based on the new principles which set in this program system TIPEX.
The elastic deformation cannot be defined in advance (with both amplitude and frequency) and put in the system but completely inversely. The elastic deformation is a dynamic value which depends on the total dynamics of the robot system movements. That means that the elastic deformation amplitude and its frequency change depending on the forces (inertial forces, Coriolis, centrifugal forces, gravity forces as well as coupling forces between the present modes, and the play of the dynamic external forces). It, of course, depends also on the mechanism configuration, weight, length of the segments of the reference trajectory choice, dynamic characteristics of the motor movements etc.
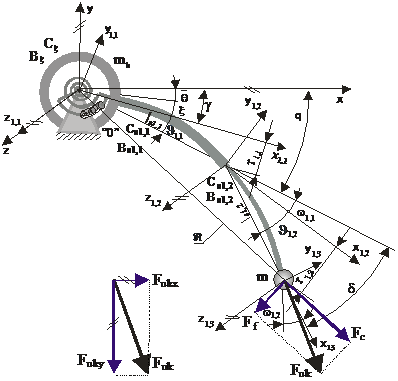
Fig. 2. Planar geometry of the mechanism in the vertical plane.
The elastic deformation exists even in the state of inaction and then it depends on the gravity forces i.e. mechanism configuration. That means that the elastic deformation depends on the robot system characteristics and it can be calculated in any chosen moment. When we conduct the mechanism through the reference trajectory, the elastic deformation also exists but now at the reference level without the influence of the disturbance.
Euler-Bernoulli equation is written in 1750. It was written by Bernoulli, physicist and Euler, mathematician, his longtime friend and colleague. They did not even dream about the robotics and the knowledge we have now on disposal. But, although it was made more than 250 years ago, the Euler-Bernoulli equation is still actual and it can be connected logically with the contemporary knowledge from the robotics.
I especially emphasize the robotics which, as we have already written, develops very intensively and in this case it imposes the solutions to the other areas such as the oscillation theory and the elasticity theory. It could have been otherwise. However, that is less important. The most important is to see the solution. It is important to establish the continuity in the researches through years, decades, centuries.
Detailed description of characteristics
The special attention is devoted to the dynamics and kinematics of movement of robotics configuration with elastic link in presence of second mode. The kinematic model of system presented on Fig. 1. and 2. (direct and inverse model) is created involving new definition of Denavit-Hartenbergs parameters. A geometric robot between internal coordinates and the space of Cartesian coordinates (external coordinates) is defined as so-called “direct kinematics”. New form of the Jacobi matrix, for a manipulator with elastic joints and links, maps the velocity vector of the external coordinates into the velocity vector of internal coordinates.
We demonstrated that the equation of motion of all the forces involved at any point (at the first mode tip on this elastic line also) follows directly from the new form Euler-Bernoulli equation. If we define boundary conditions for the mode tip as the most interesting point on the elastic line, we obtain the equation of motion at that point, what is classical form of the mathematical model. The choice of the reference trajectory, which depends on the level of the elasticity characteristics knowledge, is generated. The estimated elasticity characteristics can be included in the reference trajectory as well as in the control law.
It is pointed out that the elastic deformation is the consequence of the total robot system dynamics which is essentially different from, until now, widely used method that implies the adaptation of the “assumed modes technique”.
Euler-Bernoulli equation has been expanded from several aspects.
With elastic robotic systems, the actuator torque is opposed by the bending moment of the first elastic mode, which comes after the motor, and partly by the bending moments of other modes, which are connected in series after the motor considered. All modes coming after the motor, because of their position, exert influence on the dynamics of motor motion. The mathematical model of motor in our program system TIPEX is connected to the rest of the mechanism via the equivalent elasticity moment.
The analogue between the solution of the Euler-Bernoulli equation which Daniel Bernoulli defined in the original form (i.e. the solution of the extended form) and „the direct kinematics solution“ in the Robotics is applied.
New structures of the stiffness matrix and mathematical model of actuators appear as a consequence of the coupling between the modes of particular links.
The analogue between the source form Euler-Bernoulli equation and its solution and modern knowledge from the Robotics is presented this way in this program system TIPEX.
Using this approach, the new research prospects have been opened. This is especially important because the elasticity characteristic is a natural characteristic of a material. In certain mechanisms, the elasticity effect is seen as an unwelcome phenomenon while in other mechanisms (such as transporters); this characteristic is elementary for functioning. No matter which one of the two cases is analyzed and synthesized, it is important to define a good mathematical model in order to make possible controlled behavior.
References
[1] Mirjana Filipovic, Miomir Vukobratovic, "Modeling of Flexible Robotic Systems", Computer as a Tool, EUROCON 2005, The International Conference,Belgrade, Serbia and Montenigro, Volume 2, 2005, pp. 1196 - 1199.
[2] Mirjana Filipović „New Aspects on Formulating the Euler-Bernoulli Equation”, TEHNIKA, Savez inženjera i tehničara Srbije, Masinstvo 59, ISSN 0040-2176, (2010) 4, pp. 1-8.
[3] Mirjana Filipovic, "Relation between Euler-Bernoulli Equation and Contemporary Knowledge in Robotics”, Robotica, International Journal, Cambridge University Press, ISSN 0263-5747, online April 2011, DOI: 10.1017/S0263574711000324.
