Research Topic: Coupling Between the Biped and the Platform
We approached this subject with the objective to obtain a most realistic description of the influence of the biped motion dynamics on the dynamics of platform motion and vice versa. As a result, we give here the first precise and integral account of the phenomenon of coupling between the biped and the platform. Coupling is first explained in detail on a biped construction involving all rigid elements in contact with the platform construction with all rigid elements too. The phenomenon of coupling by itself is complex enough, and just because of that it is defined first in some simpler circumstances.
The coupling characteristics are very important, and exactly because of that their explanation should not be blurred by some other effects such as, for example, elasticity. The complex robotic mechanism consisting of the humanoid and the platform being in contact at the point A, is sketched in Figure a. The inertia matrix is a full matrix, having also elements outside the diagonal, characterizing the coupling between the present degrees-of-freedom (DOFs). The presence of coupling is also reflected on the vector through the Coriolis' and centrifugal forces. The complex system shown in Figure a is divided, first hypothetically, in two parts (Figure b), whereby the upper system can move independently of the lower one. The upper system is the biped and the lower the platform.
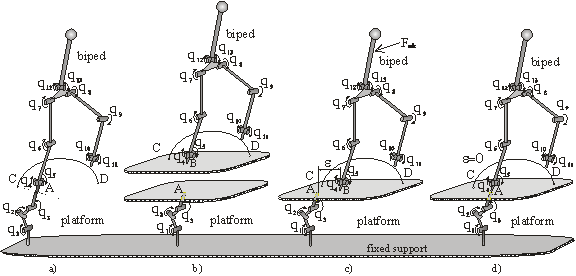
Fig. 1. Complex robotic mechanism biped-platform.
When separated, these two systems perform independent motions. As we want to analyze the motion dynamics of the biped and platform in contact, we presume exactly such a situation and because of that it is necessary to connect these two subsystems. Their linking gives the system shown in Figure c. Let us compare Figures a and c. They stand for the similar robotic configurations. It has been already mentioned that between particular (DOFs) in Figure a there exists strong coupling, and because of that it is logical to suppose that the same strong coupling exists between the particular biped DOFs and particular platform DOFs from Figure c. In general, the biped need not be in contact with the platform at the point "A" but at some other point, for example "B" (see Figure c). If the points "A" and "B" coincide, then the geometry of the overall complex mechanism is simpler. This would be a most favorable case. However, a much more realistic is the case when the points "A" and "B" do not coincide. Then there exists a quantity which participates in the dynamics of the overall system motion. Full coupling between the particular DOFs of the biped and platform is an essential characteristic of this robotic system. The inertiality matrix of the biped and platform is a full matrix, and the Coriolis' and centrifugal forces encompass also the coupling between the biped and platform.
Now, when we explained the characteristic of coupling between the biped and the platform as rigid systems, it is logical to conclude that the additional elasticity in the system (elastic joints of the humanoid and/or elastic joints of the platform) could only increases the complexity of coupling that takes place via the elasticity forces, as well as via the inertial, Coriolis' and centrifugal forces.
The introduction of elasticity elements into the already complex biped-platform system, makes it only more complex.
