Research Topic: General form of mathematical model of a humanoid locomotion system walking on immobile/mobile platform (with rigid and (or) elasticity gears)

We analyze the kinematics and dynamics of a humanoid robotic system walking on an immobile/mobile platform. Since elasticity elements are introduced, it is necessary to give first a detailed explanation of the kinematics of these systems, to make their dynamic modeling as efficient as possible. In the presence of elasticity elements, the notion of a joint (degree-of-freedom, DOF) acquires a new meaning, which needs an explanation. This means that a joint can be defined in dependence of the working state of the motor and type of gearing. We distinguish four types of joints.

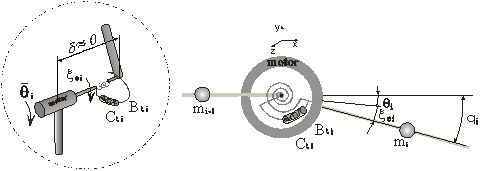
Joint of the type AE and its geometry.

Fig. 1. Joint of the type AE and its geometry.

Joint of the type LE and its geometry.

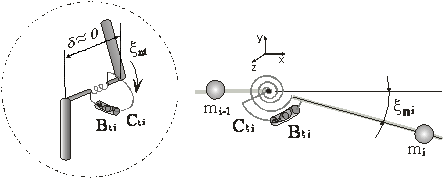
Fig. 2. Joint of the type LE and its geometry.

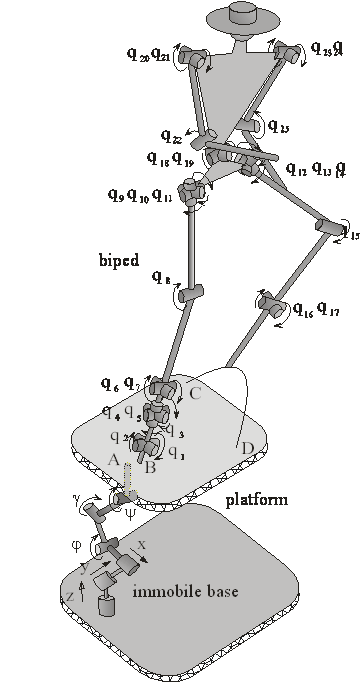
Humanoid robotic mechanism with 25 DOF and platform with 6 DOF (this example is analyzed only with flexible gears).

Fig. 3. Humanoid robotic mechanism with 25 DOF and platform with 6 DOF (this example is analyzed only with flexible gears).

The algorithm defined generates a general form of mathematical model of a complex humanoid robotic system that walks on an immobile/mobile platform. The task of modeling is solved as a program, so that the user should only select the type of joints and, all the system parameters, and the software package will generate a model which offers the possibility of analyzing its dynamic behavior.

The dynamic model of robotic mechanism encompasses all coupling elements, as well as all dynamic effects of the present forces. Elastic deformations of the elastic elements are defined as a logical consequence of dynamic load moments.

Elasticity dynamics is analyzed in dependence of the dynamics of the overall robotic system. It is shown that there exist strong coupling between the DOFs during the motion of the complex robotic system. The humanoid robotic system is described by a system of differential equations of damped oscillations.

Simulations were carried out for the case when the reference trajectory did not encompass the magnitude of elastic deformation. The software package offers comfort in the analysis of complex elastic robotic systems. The characteristic of configuration complexity of the robotic system and the choice of elasticity characteristic in the system are not any more limiting factors in the analysis of kinematics and dynamics of humanoid robotic systems. The software package includes the possibility of simulating also the example with the joints of LE type in the foot sole or platform.

Thus, an essentially new approach is elaborated for considering elastic robotic systems, which opens up some new possibilities in the analysis and modeling of these systems, as well as in the implementation of new control laws.

The paper emphasizes the existence of dynamic coupling between the biped and the platform in the course of robotic task realization. In the moment of robot's stepping on the platform, these two complex contacting systems form a more complex mechanical system. Mathematical model of the overall system must encompass all the elements of coupling between the DOFs of the biped and platform. Coupling is an elementary property of robotic systems that has to be taken into consideration when analyzing the motion of the biped and platform in contact. Simulations and analyses encompassed the dynamics of the biped walk on a mobile platform involving only rotational DOFs. Inclusion of the elementary property of coupling between the biped and the platform suggests the need for synthesizing new control laws to track the ZMP trajectory. In the case when elastic characteristics are included, the coupling becomes stronger and the departure of the real ZMP trajectory from its reference value becomes larger. It appeared that the choice of parameters (motors, configuration, geometry, elasticity characteristics, trajectory selection, etc.) of such complex biped-platform system may play an essential role in the process of system stabilization. This is only one aspect of the analysis of dynamic behavior of robotic systems which opens the door to other research aspects. Our final goal is to achieve the humanoid walking on the platform, and this will be possible if much more knowledge is gained about this complex system.

The software package, synthesized specifically for the purpose of allowing more comfortable analysis of such complex system, gave interesting simulation results. By using it, the user can choose the configuration of the system to be analyzed as well as the types of particular DOFs. Besides, there exists the possibility of expanding the software package from various aspects, to meet the user's diverse needs.

Real elastic deformations [rad].

Fig. 4. Real elastic deformations [rad].

If the platform construction includes joints of the LE type with small damping, the ZMP trajectory roams far away from the zero position, and the system becomes unstable.

Reference ZMPo and real ZMP [m].

Fig. 5. Reference ZMPo and real ZMP [m].

Reference ZMPo and real ZMP [m].

Fig. 6. Reference ZMPo and real ZMP [m].

Real elastic deformation [rad].

Fig. 7. Real elastic deformation [rad].

If for the same system configuration damping characteristic of the LE joint is increased, the system would be still oscillatory, but it would lose the tendency of being unstable.

Reference ZMPo and real ZMP [m].

Fig. 8. Reference ZMPo and real ZMP [m].